详解二叉查找树操作

二叉查找树（Binary Search Tree）又称二叉排序树、二叉搜索树。二叉查找树是为了实现快速查找而生的，一般情况下，查询效率比链表结构要高。不过，它不仅仅支持快速查找一个数据，还支持快速插入、删除一个数据。二叉查找树要求，在树中的任意一个节点都要满足，其左子树中每个节点的值，都要小于这个节点的值，而右子树每个节点的值都大于这个节点的值。二叉查找树操作主要分为查找，插入和删除，下面我们来一一介绍。

1.查找

在二叉查找树中查找一个节点，我们先取根节点，如果它等于我们要查找的数据，那就返回。如果要查找的数据比根节点的值小，那就左子树中递归查找；如果要查找的数据比根节点的值大，那就右子树中递归查找。

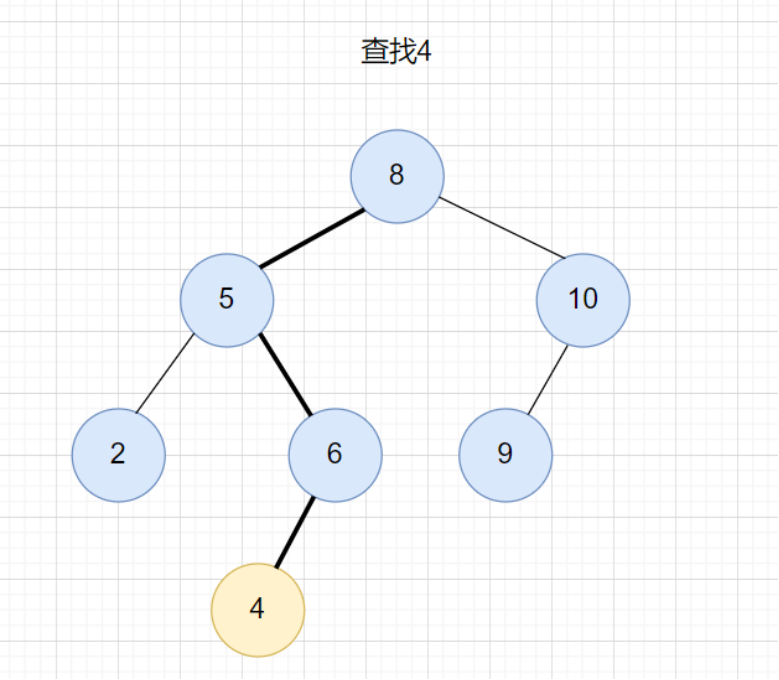
查找的代码实现:

public class BinarySearchTree {
    private Node root;
    public Node find(int data) {
        Node temp = root;
        while (temp != null) {
            if (data == temp.data) {
                return temp;
            } else if(data > temp.data) {
                temp = temp.rchild;
            } else {
                temp = temp.lchild;
            }
        }
        return null;
    }
}

public class Node {
    int data;
    Node lchild;
    Node rchild;
    public Node(int data) {
        this.data = data;
    }
}

2.插入

插入的操作类似于查找的操作。从根节点开始，依次比较要插入的数据和节点的关系。 如果要插入的数据比节点的数据大，并且节点的右子树为空，就将数据直接插入到右子节点的位置，如果右子树不为空，那就继续遍历右子树；如果要插入的数据比节点的数据小，并且节点的左子树为空，就将数据直接插入到左子节点的位置，如果左子树不为空，那就继续遍历左子树。

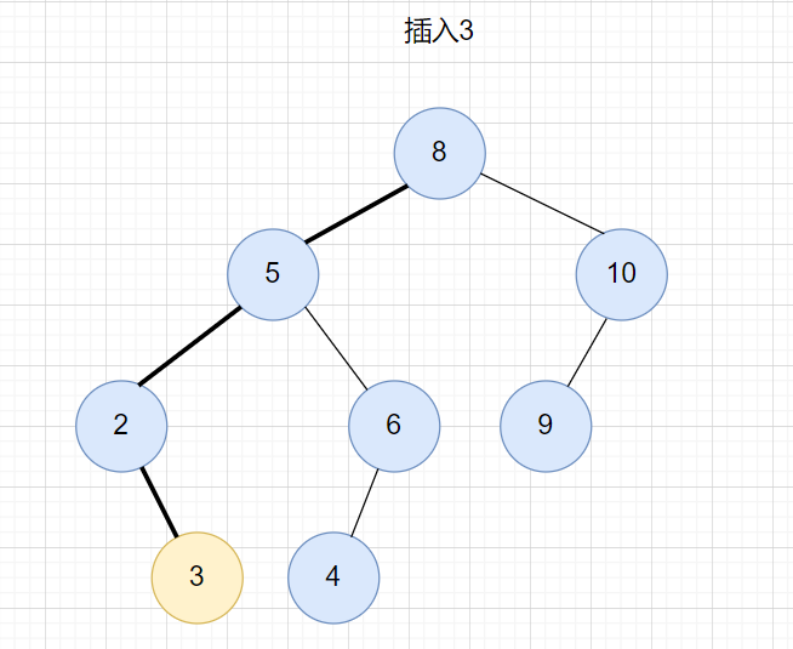
插入的代码实现:

public void insert(int data) {
        if (root == null) {
            root = new Node(data);
            return;
        }
        
        Node temp = root;
        while (true) {
            if (data > temp.data) {
                if (temp.rchild == null) {
                    temp.rchild = new Node(data);
                    return;
                }
                temp = temp.rchild;
            } else {
                if (temp.lchild == null) {
                    temp.lchild = new Node(data);
                    return;
                }
                temp = temp.lchild;
            }
        }
}

3.删除

二叉查找树的查找和插入的操作比较简单，但是删除的操作较为复杂，分为三种情况。 第一种情况，要删除的节点是叶子节点。此时只需要直接将父节点中指向要删除节点的指针置为null即可。如下图中删除28。 第二种情况，要删除的节点有只有一个子节点（左子节点或右子节点），我们只需要更新父节点中的指针，让它指向要删除节点的字节点就可以了。如下图中的34。 第三种情况，要删除的节点有两个子节点。这种情况下，我们需要把要删除节点的右子树中最小的节点替换要删除节点。如下图中的15。

删除完成后

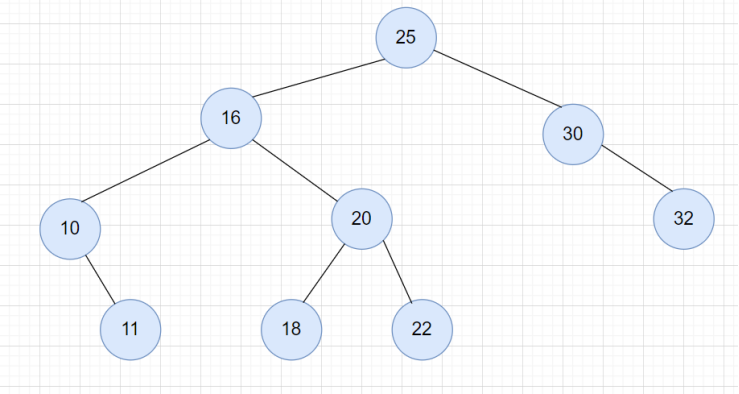
代码实现:

 public void delete(int data) {
        Node temp = root;  // temp指向要删除的节点
        Node ftemp = null; // ftemp指向要删除节点的父节点
        while (temp != null && temp.data != data) {
            ftemp = temp;
            if (data > temp.data) {
                temp = temp.rchild;
           } else {

                temp = temp.lchild;
            }
        }

       if (temp == null) return; // 没有找到对应的节点
       // 若找到，temp就是要删除的节点
       // 要删除的节点有两个子节点
        if (temp.lchild != null && temp.rchild != null) {
            Node minTemp = temp.rchild;  // 存储右子树的最小节点
            Node fminTemp = temp; // minTemp的父节点

            // 找到右子树的最小节点
            while (minTemp.lchild != null) {
                fminTemp = minTemp;
                minTemp = minTemp.lchild;
            }

            temp.data = minTemp.data; // 将最小节点的值替换到temp中
            temp = minTemp;  // 变成删除叶子节点
            ftemp = fminTemp;
        }

        // 删除节点是叶子节点或者仅有一个节点
        Node child; // temp的子节点
        if (temp.lchild != null) {
            child = temp.lchild;
        } else if (temp.rchild != null) {
            child = temp.rchild;
        } else {
            child = null;
        }

        if (ftemp == null) {  // 删除的是根节点
           root = child;

        } else if (ftemp.lchild == temp) {
            ftemp.lchild = child;
        } else {
            ftemp.rchild = child;
        }
    }

以上就是对二叉查找树操作的相关介绍，二叉查找树本质上是一棵空树，或者没有键值相等的结点，对二叉查找树的定义也是相对的。想要深入学习二叉查找树的小伙伴可以观看本站的数据结构和算法教程，积累更多关于二叉查找树的相关知识。