优先队列的详解

1.优先队列：

能够完成以下两个操作的数据结构叫优先队列：

可以插入新元素

可以快速取出所有元素的最值。

2.优先队列的实现：堆

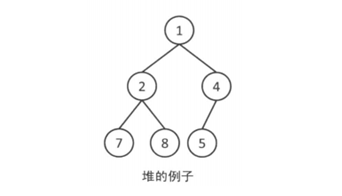
堆是一颗完全二叉树。

重要的性质：父节点一定是其所有子孙节点的最值。

一个简单的堆的示意图如下：

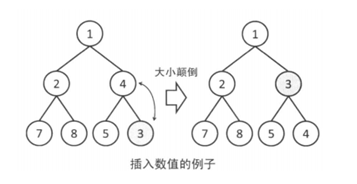
堆的插入：首先在堆的末尾插入该数值，然后不断向上调整，直到没有大小颠倒为止

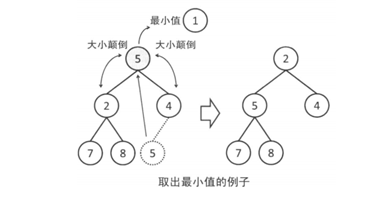
取出最值：最值就在堆顶，即二叉树的第一个元素。

删除最值：首先将堆的最后一个元素复杂到根节点，并删除最后一个元素，然后将根节点不断向下进行调整直到没有大小颠倒。

时间复杂度：堆的插入和删除的时间复杂度为O(l o g⁡n)O(log⁡n)O(log⁡n)

注意：删除和插入具体的向上/下调整的方法，可以看下面的代码。

3.代码

优先队列的实现：我们知道完全二叉是可以通过简单的数值实现的，如果我们将完全二叉树中的每个节点进行编号，编号从1开始，编号顺序是从上到下从左到右，然后根据这个编号将树中的节点存储到数组中，父子关系可以通过下面方式得到：

假设当前节点的编号(数组中的编号)为i ii，则有：

它的父节点的编号为：i/2 i/2i/2(整除)

它的左儿子节点的编号为：2∗i 2*i2∗i

它的右儿子节点的编号为：2∗i+1 2*i+12∗i+1

//最小堆的实现
#include <iostream>
#define Max_N   1005

using namespace std;

int Heap_size;
int Heap[Max_N];

//插入操作
void push(int x)
{
    int indx=++Heap_size;//首先插入到最后一个位置
    //向上调整
    while(indx>1)//只有i>1才会有父节点
    {
        int parent_indx=indx/2;//父节点编号
        if(Heap[parent_indx]<=x)//没有上下颠倒就结束调整
            break;
        Heap[indx]=Heap[parent_indx];//大小颠倒就将当前节点上调
        indx=parent_indx;

    }
    Heap[indx]=x;
}

//删除操作
int pop()
{
    int result=Heap[0];//获取最值
    int x=Heap[--Heap_size];//相当于将最后的一个元素放到根节点
    int index=1;
    while(2*index<=Heap_size)//一定要有子节点
    {
        int L_son_index=2*index;
        int R_son_index=2*index+1;
        //比较儿子节点的最值
        int Min_index=L_son_index;
        if(R_son_index<=Heap_size && Heap[R_son_index]<Heap[Min_index])
            Min_index=R_son_index;
        //如果没有上下颠倒就结束
        if(Heap[Min_index]>=x)
            break;
        //上下颠倒就交换
        Heap[index]=Heap[Min_index];
        index=Min_index;
    }
    Heap[index]=x;
    return result;
}

void Build_Heap(int data[],int n)
{
    //创建一个空堆
    Heap_size=0;
    for(int i=0;i<n;i++)//逐个插入元素
        push(data[i]);

}


int main()
{
    int n;
    int data[Max_N];
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>data[i];
    cout<<"使用下面数据构建堆"<<endl;
    for(int i=0;i<n;i++)
        cout<<data[i]<<" ";
    cout<<endl;
    Build_Heap(data,n);
    cout<<"堆中数据："<<endl;
    for(int i=1;i<=Heap_size;i++)
        cout<<Heap[i]<<" ";
    cout<<endl;
    return 0;
}
/*
9
9 7 10 4 5 19 23 6 7
*/

4.优先队列的库：

实际上，大部分情况并不需要自己使用堆来实现优先队列，我们可以使用C++中，STL里面的priority_queue来实现优先队列。

以上就是极悦小编介绍的"优先队列的详解"，希望对大家有帮助，想了解更多可查看Java教程。极悦在线学习教程，针对没有任何Java基础的读者学习,让你从入门到精通,主要介绍了一些Java基础的核心知识，让同学们更好更方便的学习和了解Java编程，感兴趣的同学可以关注一下。