线性表的顺序存储结构详解
- 2022-07-14 10:02:01
- 782次 极悦
线性表:零个或多个数据元素的有限序列
线性表的数据对象集为{a 1 , a 2 , ……, a n },每个数据元素的类型相同。其中,除了第一个元素 a1 之外,每个元素都有并且只有一个直接前驱元素,除了最后一个元素 a n之外,每个元素都有并且只有一个直接后继元素。数据元素之间的关系是一对一的。
线性表的订单存储结构
线性表的数据元素一次存储在具有连续地址的存储单元中
一个1一个2......一个i-1我_......一个_
顺序存储结构需要三个属性:
存储空间的起始位置:数据数据,其存储位置为存储空间的存储位置。
直线米最大存储容量:数组MaxSize的长度。
直线米的当前长度:长度。
内存地址计算方法
用数组存储顺序表意味着分配固定长度的数组空间,因为线性表可以插入或删除,所以分配的数组空间应该大于等于当前线性表的长度。
记忆中的地址,就像图书馆的座位一样,都是编号的。内存中的每个存储单元都有自己的编号、地址。因为是顺序结构,所以当第一个位置确定后,后面的位置就可以计算出来了。比如,我全班第五,排在我后面的是10,学生的成绩是6,7,...,15,因为5+1,5+2,...,5+10。每一个数据元素,无论是整容、真实还是人物,都需要占用一定的存储单元空间。假设占用c个存储单元,那么线性表中第二个i+1个数据元素的存储位置和i个数据元素的存储位置满足如下关系:
LOC (a i + 1 ) = LOC (a i ) + c
所以对于第 i 个数据元素 a i的存储位置可以有一个1计算得到:
LOC (a i ) = LOC (a 1 ) + (i-1) * c
通过这个公式,可以同时计算出线性表中任意位置的地址,任意位置,全部。它的时间复杂度是 O(1)。一般将具有这种特性的存储结构称为随机存取结构。
顺序存储结构的插入和删除
1.获取元素操作码:
public class ArrayList<E> {
transient Object[] elementData;
public E get(int index) {
Objects.checkIndex(index, this.size);
return this.elementData(index);
}
E elementData(int index) {
return this.elementData[index];
}
}
Copy code
2.插入
比如,买春运火车票。每个人都排好队。这位是美女,说……对排队的第三个人,“大哥,请帮帮我,我妈在家病了,赶紧回去看看她,队伍这么长,能不能把我放进去在你面前?”你心软,答应了。身后的人都不得不退后一步。这个例子实际上已经说明了线性表的顺序存储结构,插入数据时的实现过程。
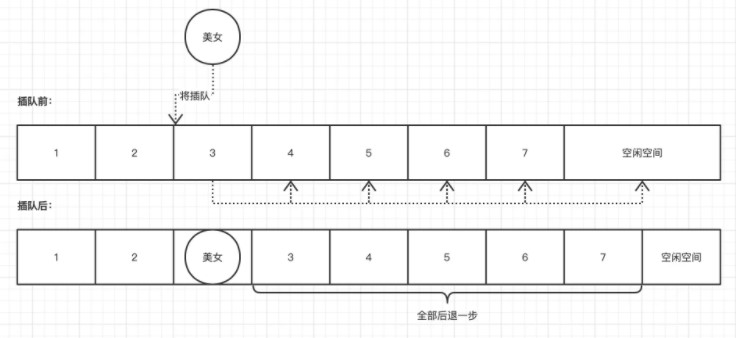
插入思路:
如果插入位置不合理,抛出异常;
如果线性表长度大于等于数组长度,则抛出异常或动态增加容量;
从最后一个元素开始,向前遍历到下一个 i A 地方,将它们分别向后移动一个位置;
填入要插入元素的位置i,Watch长度加1。
代码实现:
public boolean add(E e) {
++this.modCount;
this.add(e, this.elementData, this.size);
return true;
}
public void add(int index, E element) {
this.rangeCheckForAdd(index);
++this.modCount;
int s;
Object[] elementData;
if ((s = this.size) == (elementData = this.elementData).length) {
elementData = this.grow();
}
System.arraycopy(elementData, index, elementData, index + 1, s - index);
elementData[index] = element;
this.size = s + 1;
}
Copy code
3.删除操作
接下来,我们以上面的例子为例。这时,一名警察出现了,对美女说道:“跟我去局。” 女人离开了队伍。原来,她是个卖火车票的黄牛,装穷排队买票。然后排队的人,都往前迈了一步。这是在线性表的顺序存储结构中删除元素的过程。
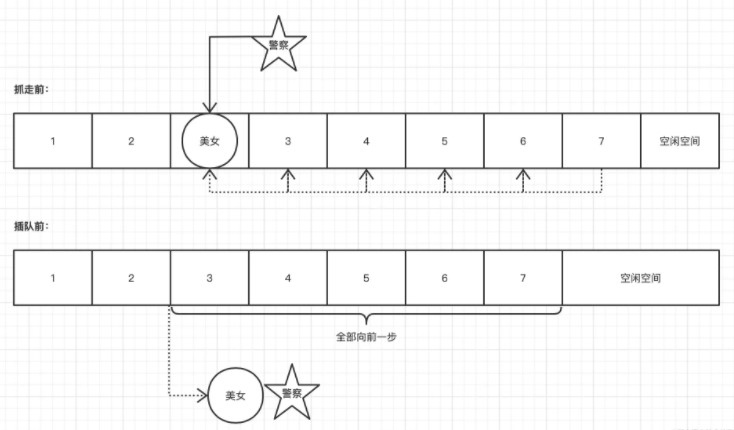
删除想法:
如果删除位置不合理,则抛出异常;
移除删除元素;
从被删除元素位置遍历到最后一个元素位置,分别向前移动一个位置;
手表长度减 1。
代码实现:
public E remove(int index) {
Objects.checkIndex(index, this.size);
Object[] es = this.elementData;
E oldValue = es[index];
this.fastRemove(es, index);
return oldValue;
}
Copy code
插入和删除的时间复杂度。
最好的情况,如果要将元素插入到最后一个位置,或者删除最后一个元素,此时时间复杂度为O(1),因为不需要移动元素。
最坏的情况,如果要插入元素到第一个位置或者要删除第一个元素,此时时间复杂度为O(n),因为它向后或向前移动了1个位置之后的所有元素。
至于一般情况,因为元素插入到了第i个A地方,或者删除了第i个元素,需要移动ni个元素。根据概率原理,在每个位置插入或删除元素的可能性是相同的,也就是说,位置在前面,移动更多元素,位置向后,移动元素更少。最终平均移动次数等于中间元素的移动次数,乘以(n-1)/2,即O(n)。
分析表明,线性表的顺序存储结构,在存在、读取数据时,无论在哪里,时间复杂度为零O(1);插入或删除时,时间复杂度为零O(n)。说明它更适合,元素数量不变,访问数据的应用也更多。
线性表顺序存储结构的优缺点
优势 :
无需为表中元素之间的逻辑关系增加额外的存储空间
您可以快速检索表格中任何位置的元素
缺点:
插入和删除操作需要移动大量元素
当延米长度变化较大时,存储空间的容量难以确定
创造存储空间“碎片”
以上就是关于“线性表的顺序存储结构详解”的介绍,大家如果对此比较感兴趣,想了解更多相关知识,不妨来关注一下极悦的Java极悦在线学习,里面的课程内容从入门到精通,很适合没有基础的小伙伴学习,希望对大家能够有所帮助。
选你想看
你适合学Java吗?4大专业测评方法
代码逻辑 吸收能力 技术学习能力 综合素质
先测评确定适合在学习
价值1998元实验班免费学












 在线咨询
在线咨询
 免费试学
免费试学