快速排序算法详解
- 2022-10-19 10:13:09
- 817次 极悦
在本文中,我们将讨论快速排序算法。快速排序的工作程序也很简单。
排序是一种以系统方式排列项目的方式。快速排序是广泛使用的排序算法,它在平均情况下进行n log n比较,以对 n 个元素的数组进行排序。它是一种更快、更高效的排序算法。该算法遵循分而治之的方法。分而治之是一种将算法分解为子问题,然后解决子问题,并将结果组合在一起以解决原始问题的技术。
Divide:在 Divide 中,首先选择一个枢轴元素。之后,将数组划分或重新排列为两个子数组,使得左子数组中的每个元素都小于或等于枢轴元素,而右子数组中的每个元素都大于枢轴元素。
征服:递归地,使用快速排序对两个子数组进行排序。
组合:组合已经排序的数组。
快速排序选择一个元素作为枢轴,然后围绕选择的枢轴元素对给定数组进行分区。在快速排序中,一个大数组被分成两个数组,其中一个保存小于指定值(枢轴)的值,另一个数组保存大于枢轴的值。
之后,左右子阵列也使用相同的方法进行分区。它将继续,直到单个元素保留在子数组中。
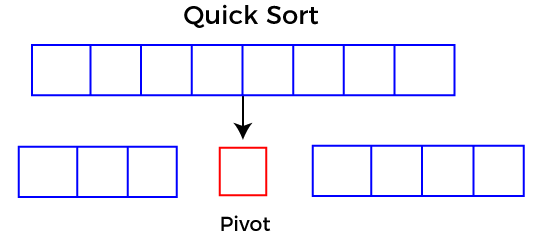
选择支点
选择一个好的支点对于快速实现快速排序是必要的。但是,通常确定一个好的支点。选择支点的一些方法如下 -
枢轴可以是随机的,即从给定数组中选择随机枢轴。
Pivot 可以是给定数组最左边元素的最右边元素。
选择中位数作为枢轴元素。
算法
算法:
QUICKSORT(数组 A,开始,结束)
{
如果 (开始 < 结束)
{
p = 分区(A,开始,结束)
QUICKSORT(A,开始,p - 1 )
QUICKSORT (A, p + 1 , 结束)
}
}
分区算法:
分区算法将子数组重新排列在一个地方。
PARTITION (array A, start, end)
{
pivot ? A[end]
i ? start-1
for j ? start to end -1 {
do if (A[j] < pivot) {
then i ? i + 1
swap A[i] with A[j]
}}
swap A[i+1] with A[end]
return i+1
}
快速排序算法的工作
现在,让我们看看快速排序算法的工作原理。
为了理解快速排序的工作原理,让我们看一个未排序的数组。它将使概念更加清晰和易于理解。
让数组的元素是

在给定的数组中,我们将最左边的元素视为枢轴。因此,在这种情况下,a[left] = 24、a[right] = 27 和 a[pivot] = 24。
由于枢轴在左侧,因此算法从右侧开始并向左移动。
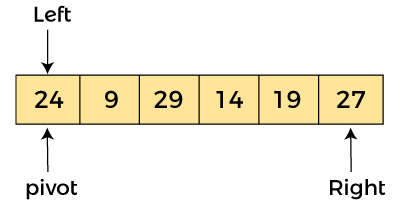
现在,a[pivot] < a[right],所以算法向左移动一个位置,即
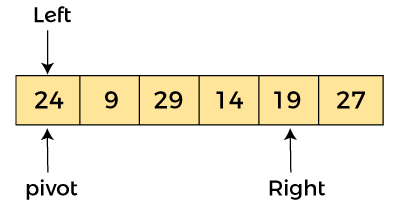
现在,a[left] = 24,a[right] = 19,a[pivot] = 24。
因为,a[pivot] > a[right],所以,算法将 a[pivot] 与 a[right] 交换,并且枢轴向右移动,如
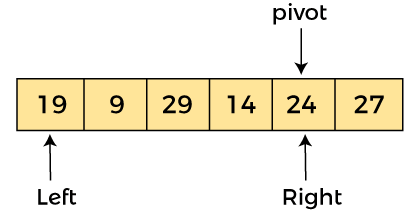
现在,a[left] = 19、a[right] = 24 和 a[pivot] = 24。由于枢轴在右侧,所以算法从左开始并向右移动。
由于 a[pivot] > a[left],所以算法向右移动一个位置
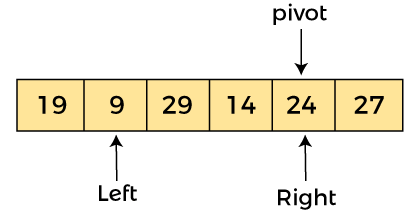
现在,a[left] = 9,a[right] = 24,a[pivot] = 24。由于 a[pivot] > a[left],所以算法向右移动一个位置
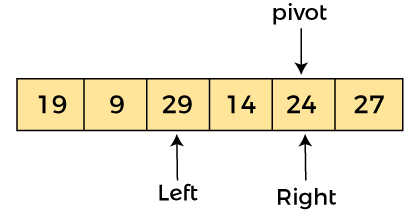
现在,a[left] = 29、a[right] = 24 和 a[pivot] = 24。由于 a[pivot] < a[left],所以,交换 a[pivot] 和 a[left],现在进行枢轴在左边,即
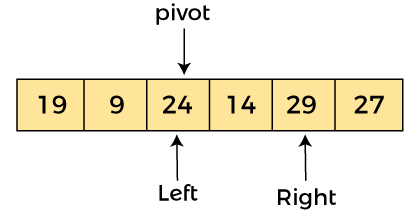
由于枢轴在左侧,因此算法从右侧开始,然后向左移动。现在,a[left] = 24,a[right] = 29,a[pivot] = 24。由于 a[pivot] < a[right],所以算法向左移动一个位置,如
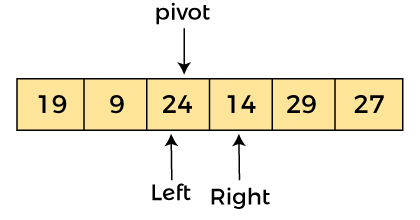
现在,a[pivot] = 24、a[left] = 24 和 a[right] = 14。由于 a[pivot] > a[right],所以,交换 a[pivot] 和 a[right],现在进行 pivot在右边,即
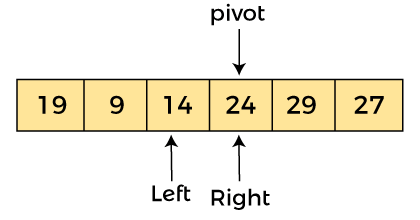
现在,a[pivot] = 24,a[left] = 14,a[right] = 24。pivot 在右边,所以算法从左开始向右移动。
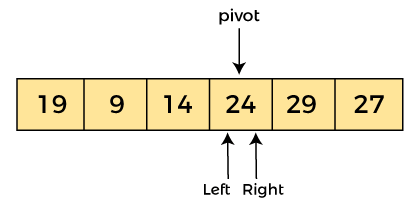
现在,a[pivot] = 24、a[left] = 24 和 a[right] = 24。因此,pivot、left 和 right 指向同一个元素。它代表程序的终止。
作为枢轴元件的元件24被放置在其确切位置。
元素 24 右侧的元素大于它,元素 24 左侧的元素小于它。
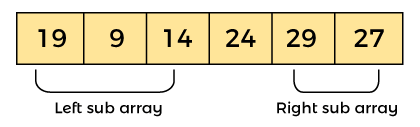
现在,以类似的方式,快速排序算法分别应用于左右子数组。排序完成后,数组将是

快速排序复杂度
现在,让我们看看快速排序在最佳情况、平均情况和最坏情况下的时间复杂度。我们还将看到快速排序的空间复杂度。
1.时间复杂度
最佳情况复杂性 -在快速排序中,当枢轴元素是中间元素或靠近中间元素时会出现最佳情况。快速排序的最佳时间复杂度是O(n*logn)。
平均案例复杂度 -当数组元素处于混乱的顺序,没有正确升序和降序时,就会发生这种情况。快速排序的平均案例时间复杂度为O(n*logn)。
最坏情况复杂性 -在快速排序中,当枢轴元素是最大或最小元素时会发生最坏情况。假设,如果枢轴元素始终是数组的最后一个元素,最坏的情况将发生在给定数组已经按升序或降序排序的情况下。快速排序的最坏情况时间复杂度是O(n 2 )。
尽管快速排序的最坏情况复杂度比合并排序和堆排序等其他排序算法要高,但在实践中它仍然更快。快速排序中最坏的情况很少发生,因为通过更改枢轴的选择,它可以以不同的方式实现。通过选择正确的枢轴元素可以避免快速排序中的最坏情况。
2. 空间复杂度
快速排序的空间复杂度为 O(n*logn)。
快速排序的实现
现在,让我们看看不同编程语言的快速排序程序。
程序:编写程序以在 Java 中实现快速排序。
公共课 快速
{
/* 将最后一个元素视为枢轴的函数,
将枢轴放在其确切位置,并放置
枢轴左侧的较小元素和较大的元素
枢轴右侧的元素。*/
int 分区 ( int a[], int start, int end)
{
int pivot = a[end]; // 枢轴元素
int i = (开始 - 1 );
for ( int j = start;j <= end - 1 ;j++)
{
// 如果当前元素小于枢轴
如果 (a[j] < 枢轴)
{
我++; // 增加较小元素的索引
int t = a[i];
a[i] = a[j];
a[j] = t;
}
}
整数 t = a[i+ 1 ];
a[i+ 1 ] = a[结束];
a[结束] = t;
返回 (i + 1 );
}
/* 实现快速排序的函数 */
void quick( int a[], int start, int end) /* a[] = 要排序的数组,start = 起始索引,end = 结束索引 */
{
如果 (开始<结束)
{
int p = 分区(a,开始,结束); //p是分区索引
快速(a,开始,p - 1 );
快速(a,p + 1 ,结束);
}
}
/* 打印数组的函数 */
void printArr( int a[], int n)
{
诠释 我;
对于 (i = 0 ; i < n; i++)
System.out.print(a[i] + " " );
}
公共静态无效 主要(字符串[]参数){
int a[] = { 13 , 18 , 27 , 2 , 19 , 25 };
int n = a.length;
System.out.println( "\n排序前的数组元素为-" );
快速 q1 = new Quick();
q1.printArr(a, n);
q1.quick(a, 0 , n - 1 );
System.out.println( "\n排序后的数组元素为-" );
q1.printArr(a, n);
System.out.println();
}
}
输出
执行上述代码后,输出将是

以上就是关于“快速排序算法详解”的介绍,算法还有很多,本站的数据结构和算法教程中找到合适的案例,加强我们对各种排序算法的理解。
选你想看
你适合学Java吗?4大专业测评方法
代码逻辑 吸收能力 技术学习能力 综合素质
先测评确定适合在学习
价值1998元实验班免费学












 在线咨询
在线咨询
 免费试学
免费试学