非递归遍历二叉树的3种方法
- 2022-12-01 10:37:13
- 960次 极悦
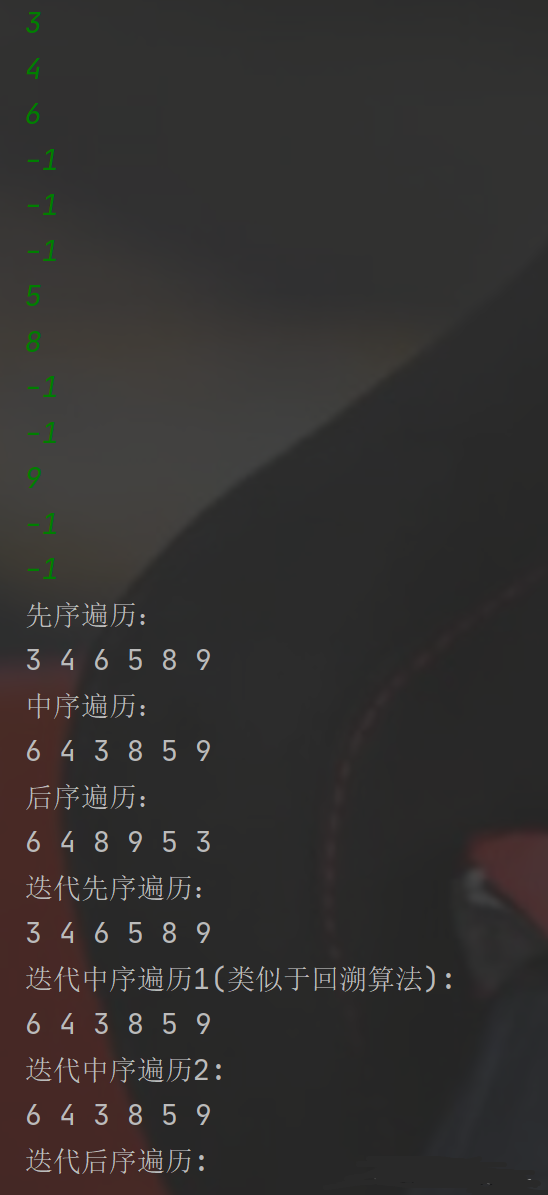
先序遍历:先序遍历结果为3 4 6 5 8 9,就拿树的左枝为例,3是根,打印,4是3的左孩子,打印,6是4的左孩子,打印,6的左孩子为空,所以返回到4,然后去找4的右孩子,4的右孩子也为空,返回到3,这就是左子树遍历的过程。然后非递归主要用到栈来存储结点,栈先进后出,所以应该是右孩子先入栈,左孩子后入栈,这样pop就能先得到左孩子。先将根结点3入栈,接下来就是开始循环,循环结束的条件就是栈为空,先弹出栈顶,再打印栈顶,如果栈顶的右孩子不为null,就把右孩子放进栈中,如果栈顶的左孩子不为null,就把左孩子放入栈中。
void pretravel2(TreeNode root) {
if (root == null) return;
Stack<TreeNode> s = new Stack<TreeNode>();
s.push(root);
while (!s.isEmpty()) {
TreeNode node = s.pop();
System.out.print(node.val+" ");
if (node.right != null) {
s.push(node.right);
}
if (node.left != null) {
s.push(node.left);
}
}
}
中序遍历:中序遍历的结果为6 4 3 8 5 9,其实就是左遍历完了,弹出根,找根的右结点,整个过程是先一路找左结点,找到左结点为null的6,然后找6的根4,接着找4的右,为null,接着找4的根3,接着一路找3的左,直到结点的左孩子为null,这就找到了8,然后找8的根5,再找5的右9,这样就找完了。他们的入栈出栈顺序:根结点入栈,左孩子直接入栈,并且标记这个结点已经走过,以防后面再走,当发现哪个结点的左孩子为null的时候,就打印这个结点,并且将这个结点出栈,让他的右孩子入栈。
void intravel2(TreeNode root) {
if(root==null)
return ;
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
//使用list来标记结点是否走过
List<TreeNode> list=new ArrayList<>();
while(!stack.isEmpty()) {
//只需要拿到根结点,不需要pop出来
TreeNode peek = stack.peek();
//如果左孩子不为null并且左孩子没有被走过,就把他放到栈里,并且标记为走过
if(peek.left!=null&& !list.contains(peek.left)) {
stack.push(peek.left);
list.add(peek.left);
}
else {//左孩子为空,打印根结点,根结点出栈,右孩子进栈
TreeNode pop = stack.pop();
System.out.print(pop.val+" ");
if(pop.right!=null)
stack.push(pop.right);
}
}
}
中序遍历还有另外一种写法:
void intravel3(TreeNode root) {
Stack<TreeNode> stack=new Stack<>();
TreeNode p=root;
while(p!=null||!stack.isEmpty()) {
while(p!=null) {
stack.push(p);
p=p.left;
}
//左孩子遍历完了,根结点弹出,打印根结点,遍历右孩子
if(!stack.isEmpty()) {
TreeNode temp=stack.pop();
System.out.print(temp.val+" ");
p=temp.right;
}
}
}
后序遍历: 后序遍历的结果为6 4 8 9 5 3,一路找左结点到6,然后找到右孩子为null,退到根4,4的右为null,然后3的左孩子遍历完了,到右孩子,一路找左孩子到8,右孩子9,根5,右孩子遍历完,最后到4。他们的进栈出栈顺序为:根结点入栈,左孩子一路入栈,当有个结点的左孩子为null的时候,就将它的右孩子入栈,如果右孩子也为null,才打印根结点。
void postrval2(TreeNode root) {
if(root==null)
return ;
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
List<TreeNode> list=new ArrayList<>();
while(!stack.isEmpty()) {
TreeNode peek=stack.peek();
//先一路走左,左走完了才到右
if(peek.left!=null&&!list.contains(peek.left)) {
//如果左结点不为null并且左结点没有走过
//就将其压入栈中,并且标记已经走过
stack.push(peek.left);
list.add(peek.left);
}
else {
if(peek.right!=null&&!list.contains(peek.right)) {
//如果右结点为不为null并且右结点没有走过
//就将右结点压入栈中,标记已经走过
stack.push(peek.right);
list.add(peek.right);
}
else {
//如果右孩子为null,就打印根结点
TreeNode pop = stack.pop();
System.out.print(pop.val+" ");
}
}
}
}
递归遍历,非递归遍历的代码
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
import java.util.*;
class TreeNode {
int val;
TreeNode left=null;
TreeNode right=null;
TreeNode(){}
TreeNode(int val) {
this.val=val;
}
}
public class Main {
public static void main(String[] args) {
Main main = new Main();
TreeNode root=null;
root=main.createTree();
System.out.println("先序遍历:");
main.pretravel(root);
System.out.println("");
System.out.println("中序遍历:");
main.intravel(root);
System.out.println("");
System.out.println("后序遍历:");
main.postravel(root);
System.out.println("");
System.out.println("迭代先序遍历:");
main.pretravel2(root);
System.out.println("");
System.out.println("迭代中序遍历1(类似于回溯算法):");
main.intravel2(root);
System.out.println("");
System.out.println("迭代中序遍历2:");
main.intravel3(root);
System.out.println("");
System.out.println("迭代后序遍历:");
main.postrval2(root);
System.out.println("");
System.out.println("层序遍历:");
main.levelOrder(root);
}
//建树
TreeNode createTree(){
Scanner sc=new Scanner(System.in);
int temp=sc.nextInt();
if(temp<=0)return null;
TreeNode root=new TreeNode();
root.val=temp;
root.left=createTree();
root.right=createTree();
return root;
}
//先序
void pretravel(TreeNode root){
if(root==null)return;
System.out.print(root.val+" ");
pretravel(root.left);
pretravel(root.right);
}
//中序
void intravel(TreeNode root){
if(root==null)return;
intravel(root.left);
System.out.print(root.val+" ");
intravel(root.right);
}
//后序
void postravel(TreeNode root){
if(root==null)return;
postravel(root.left);
postravel(root.right);
System.out.print(root.val+" ");
}
//迭代先序
void pretravel2(TreeNode root) {
if (root == null) return;
Stack<TreeNode> s = new Stack<TreeNode>();
s.push(root);
while (!s.isEmpty()) {
TreeNode node = s.pop();
System.out.print(node.val+" ");
if (node.right != null) {
s.push(node.right);
}
if (node.left != null) {
s.push(node.left);
}
}
}
void intravel2(TreeNode root) {
if(root==null)
return ;
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
List<TreeNode> list=new ArrayList<>();
while(!stack.isEmpty()) {
TreeNode peek = stack.peek();
if(peek.left!=null&& !list.contains(peek.left)) {
stack.push(peek.left);
list.add(peek.left);
}
else {//左孩子为空,打印根结点,根结点出栈,右孩子进栈
TreeNode pop = stack.pop();
System.out.print(pop.val+" ");
if(pop.right!=null)
stack.push(pop.right);
}
}
}
void intravel3(TreeNode root) {
Stack<TreeNode> stack=new Stack<>();
TreeNode p=root;
while(p!=null||!stack.isEmpty()) {
while(p!=null) {
stack.push(p);
p=p.left;
}
if(!stack.isEmpty()) {
TreeNode temp=stack.pop();
System.out.print(temp.val+" ");
p=temp.right;
}
}
}
void postrval2(TreeNode root) {
if(root==null)
return ;
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
List<TreeNode> list=new ArrayList<>();
while(!stack.isEmpty()) {
TreeNode peek=stack.peek();
if(peek.left!=null&&!list.contains(peek.left)) {
stack.push(peek.left);
list.add(peek.left);
}
else {
if(peek.right!=null&&!list.contains(peek.right)) {
stack.push(peek.right);
list.add(peek.right);
}
else {
TreeNode pop = stack.pop();
System.out.print(pop.val+" ");
}
}
}
}
//层序
void levelOrder(TreeNode root) {
List<TreeNode> list=new ArrayList<>();
list.add(root);
while(list.size()!=0) {
TreeNode temp=list.get(0);
if(temp.left!=null) list.add(temp.left);
if(temp.right!=null) list.add(temp.right);
list.remove(0);
System.out.print(temp.val+" ");
}
}
}
输入是按照先序序列输,输一个打一个回车,结点为null的时候输入-1,表示为空,叶子节点要输两个-1,表示左右孩子均为空。

以上就是关于“非递归遍历二叉树的3种方法”的介绍,本站的数据结构和算法教程对二叉树遍历方式有非常详细的讲解,不需要我们过多的推导,但我们学习的时候应该更注重理解,这样才能够学有所思。
选你想看
你适合学Java吗?4大专业测评方法
代码逻辑 吸收能力 技术学习能力 综合素质
先测评确定适合在学习
价值1998元实验班免费学












 在线咨询
在线咨询
 免费试学
免费试学