递归算法时间复杂度的分析
- 2022-12-16 10:28:53
- 886次 极悦
递归算法时间复杂度的分析,小编来举例说明。大家来看一下这道面试题:求x的n次方
大家想一下这么简单的一道题目代码应该如何写。
最直观的方式应该就是,一个for循环求出结果,代码如下
int function1(int x, int n) {
int result = 1; // 注意 任何数的0次方等于1
for (int i = 0; i < n; i++) {
result = result * x;
}
return result;
}
时间复杂度为O(n)
此时面试官会说,有没有效率更好的算法呢。
如果同学们此时没有思路,建议不要说:我不会,我不知道。可以和面试官探讨一下,问:可不可以给点提示。
面试官一般会提示:考虑一下递归算法
有的同学就写出了如下这样的一个递归的算法,使用递归解决了这个问题
int function2(int x, int n) {
if (n == 0) {
return 1; // return 1 同样是因为0次方是等于1的
}
return function2(x, n - 1) * x;
}
面试官问:那么这份代码的时间复杂度是多少?
有的同学可能一看到递归就想到了logn,其实并不是这样
递归算法的时间复杂度本质上是要看: 递归的次数 * 每次递归中的操作次数
那我们再来看代码,我们递归了几次呢。
每次n-1,递归了n次 时间复杂度是O(n),每次进行了一个乘法操作,乘法操作的时间复杂度一个常数项O(1)
所以这份代码的时间复杂度是 n * 1 = O(n)
这个时间复杂度可能就没有达到面试官的预期。
于是同学又写出了这样的一个递归的算法的代码如下 ,来求 x的n次方
int function3(int x, int n) {
if (n == 0) {
return 1;
}
if (n % 2 == 1) {
return function3(x, n/2) * function3(x, n/2)*x;
}
return function3(x, n/2) * function3(x, n/2);
}
面试官看到后微微一笑,问这份代码的时间复杂度又是多少呢?
我们来分析一下
首先看递归了多少次呢,可以把递归的次数 抽象出一颗满二叉树。
我们刚刚写的这个算法,可以用一颗满二叉树来表示(为了方便表示 我选择n为偶数),如图:
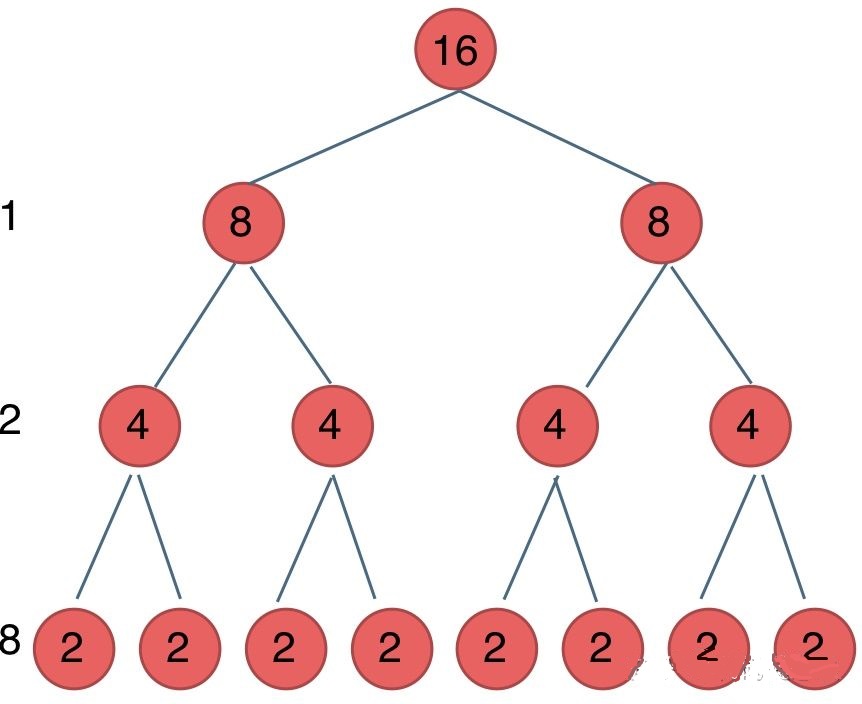
当前这颗二叉树就是求x的n次方,n为16的情况
n为16的时候 我们进行了多少次乘法运算呢
这棵树上每一个节点就代表着一次递归并进行了一次相乘操作
所以 进行了多少次递归的话,就是看这棵树上有多少个节点。
熟悉二叉树的同学应该知道如何求满二叉树节点数量
这颗满二叉树的节点数量就是2^3 + 2^2 + 2^1 + 2^0 = 15
有同学就会发现 这其实是等比数列的求和公式, 如果不理解的同学可以直接记下来这个结论。
这个结论在二叉树相关的面试题里也经常出现。
这么如果是求x的n次方,这个递归树有多少个节点呢,如下图所示
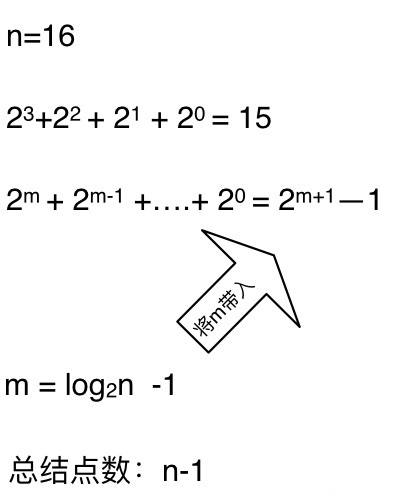
时间复杂度忽略掉常数项-1之后,我们发现这个递归算法的时间复杂度依然是O(n)。
此时面试官就会问, 貌似这个递归的算法依然还是O(n)啊, 很明显没有达到面试官的预期
那么在思考一下 O(logn)的递归算法应该怎么写
这里在提示一下 上面刚刚给出的那份递归算法的代码,是不是有哪里比较冗余呢。
来看这份优化后的递归算法代码
int function4(int x, int n) {
if (n == 0) {
return 1;
}
int t = function4(x, n/2);// 这里相对于function3,是把这个递归操作抽取出来
if (n % 2 == 1) {
return t*t*x;
}
return t*t;
}
那我们看一下 时间复杂度是多少
依然还是看他递归了多少次
我们可以看到 这里仅仅有一个递归调用,且每次都是 n/2
所以这里我们一共调用了 log以2为底n的对数次
每次递归了做都是一次乘法操作,这也是一个常数项的操作,
所以说这个递归算法的时间复杂度才是真正的O(logn)。
以上就是关于“递归算法时间复杂度的分析”介绍,大家如果对此比较感兴趣,想了解更多相关知识,不妨来关注一下本站的Java算法视频教程,里面的课程内容细致全面,通俗易懂,很适合没有基础的小伙伴学习,希望对大家能够有所帮助。
选你想看
你适合学Java吗?4大专业测评方法
代码逻辑 吸收能力 技术学习能力 综合素质
先测评确定适合在学习
价值1998元实验班免费学












 在线咨询
在线咨询
 免费试学
免费试学