深入解析递归算法
- 2020-12-10 17:43:45
- 1613次 极悦
在算法的实现中,遍历与递归是经常出现的两种操作。遍历其实就是使用一个for循环来遍历集合里的元素,在编程中经常出现,通俗易懂,至于递归,我们先来看看递归的概念:在数学与计算机科学中,是指在函数的定义中使用函数自身的方法。其实递归在程序语言中简单的理解就是方法自己调用自己。递归其实和循环是非常像的,循环都可以改写成递归,递归未必能改写成循环,这是一个充分不必要的条件。今天这篇文章就带大家深入解析递归算法。
递归做为一种算法在程序设计语言中广泛应用。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
构成递归需具备的条件:
1. 子问题须与原始问题为同样的事,且更为简单;
2. 不能无限制地调用本身,须有个出口,化简为非递归状况处理。
通过使用递归,可以把一个大型复杂的问题逐层转化为一个与原问题相似的规模较小的问题来求解。因此如果使用递归,可以达到使用少量的代码就可描述出解题过程所需的多次重复计算的目的,减少了程序的代码量 。
下面用一个例子来具体感受一下递归操作:
大家应该都比较熟悉阶乘的算法:3!= 3 * 2 * 1 ; 4!= 4 * 3 * 2 * 1
不难看出,在这里反复执行了一个逐渐-1和相乘的操作,如果可以使用某段代码达到重复调用的效果就很方便了,在这里就可以使用递归:
func factorial(_ n:Int) -> Int{
return n < 2 ? 1: n * factorial(n-1)
}
factorial(3) //6
在上面的代码里,factorial函数调用了它自己,并且在n<2的时候返回了1;否则继续调用自己。从代码本身其实不难理解函数调用的方式,但是这个6究竟是怎么算出来的呢?这就涉及到递归的实现原理了。
递归的调用实际上是通过调用栈(callback stack)来实现的,为了加深我们的理解可结合下图来看:
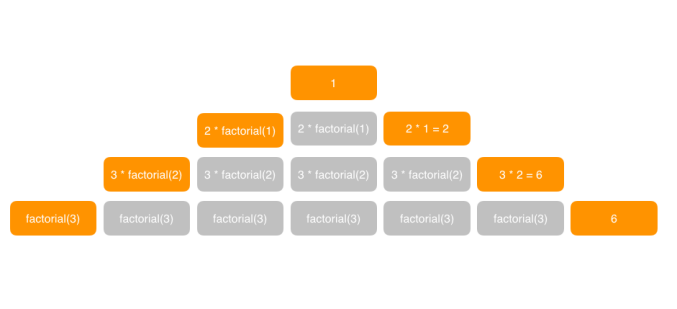
由上图可以看出,整个递归的过程和栈的入栈出栈的操作非常类似:橘黄色背景的圆角矩形代表了栈顶元素,也就是正在执行的操作,而灰色背景的圆角矩形则代表了其余的元素,它们的顺序就是当初被调用的顺序,而且在内容上保持了当时被调用时执行的代码。
现在我们按照时间顺序从左到右来说明一下整个调用的过程:
最开始传入3之后,3满足了n>=2的条件,继续调用自己:3 * factorial(2) ,入栈。
传入2之后,2满足了n>=2的条件,继续调用自己:2 * factorial(1) ,入栈。
传入1之后,1满足了n<2的条件,停止调用自己,返回了1,出栈。
此时的栈顶元素为2 * factorial(1) ,而刚刚factorial(1)返回了1,所以现在这里变成了2 * 1 = 2,出栈。
同样地,此时栈顶元素为3 * factorial(2)里的 factorial(2)返回了2,所以现在这里变成了3 * 2 = 6,出栈。
最后,factorial(3)返回了6,出栈,递归结束。
整个递归的过程可以大致理解为:在使递归继续的条件为false之前,持续递归调用,以栈的形式保存调用上下文(临时变量,函数等)。一旦这个条件变为true,则立即按照出栈的顺序(入栈顺序的逆序)来返回值,逐个传递,最终传递到最开始调用的那一层返回最终结果。再简单点,递归中的“递”就是入栈,传递调用信息;“归”就是出栈,输出返回值。
而这个分界线就是递归的终止条件。很显然,这个终止条件在整个递归过程中起着举足轻重的作用。试想一下,如果这个条件永远不会改变,那么就会一直入栈,就会发生栈溢出的情况。事实上,递归算法解题相对常用的算法如普通循环等,运行效率较低。因此,在有选择的情况下不建议使用递归算法。到这里关于深入解析递归算法的所有问题,就讲完了,希望大家对于递归的知识有所掌握和了解,如果对递归相关的知识还有其它问题,我们可以在本站的数据结构和算法教程中学习更多的优秀算法,让我们在解题有更多的选择。
选你想看
你适合学Java吗?4大专业测评方法
代码逻辑 吸收能力 技术学习能力 综合素质
先测评确定适合在学习
价值1998元实验班免费学












 在线咨询
在线咨询
 免费试学
免费试学