浅谈二叉树中序遍历
- 2021-02-03 17:34:11
- 1479次 极悦
由于二叉树是非线性结构,因此,树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。先序、中序、后序遍历二叉树的区别在于:根节点被访问的先后。也就是每种遍历方式的按自己独特的规则和顺序走遍二叉树的所有结点,使每一个结点都被访问一次,而且只被访问一次。本文我们主要来探讨一下二叉树中序遍历。
先访问根节点再访问其左右子树,这是先序遍历;按照左子树、根节点、右子树的顺序访问的方式便为中序遍历;那么后序遍历,自然就是先访问左右子树,再访问根节点了。二叉树的三种遍历方式其实思想都是一样的,掌握了一种就可以举一反三。
中序遍历递归写法很简单,就是直接按照定义来实现就 OK 了。
status Mid_view_root(BTpoint T,status (*view)(TElemType e)) //中序遍历的递归写法
{
if(T!=NULL)
{
if(Mid_view_root(T->lchild,view))
if(Print_tree_data(T->data))
if(Mid_view_root(T->rchild,view))
return OK;
return ERROR;
}
else return OK;
}
那么中序遍历的非递归形式该怎么写呢?
首先,中序遍历(非递归)得用到「 栈 」这种数据结构。栈的特点是:先进后出,我们也正是利用了这个特点来实现中序遍历的非递归形式。
那么,这又是如何实现的呢?
先遍历二叉树的根节点的左子树到最后一个左子树节点,按顺序将它们入栈;出栈并输出最后一个左子树节点;读取该节点的右子树,重复上述操作。如果一个结点的左右子树都被访问过,则退回到该节点的父结点,将其输出,读取右子树。如此循环,最后就能得到中序遍历(非递归)的输出了。
假设有这么一棵二叉树:
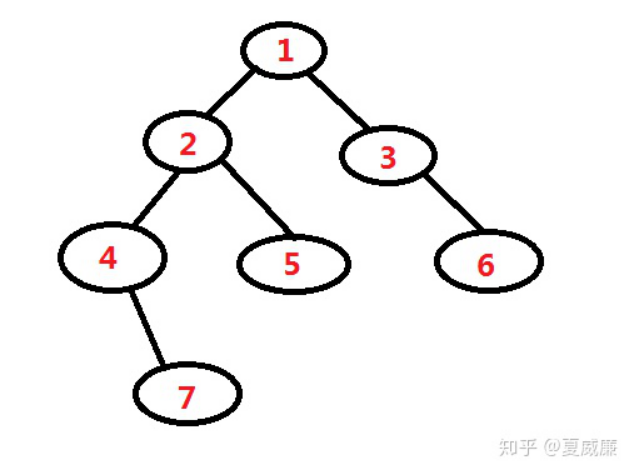
首先,结点「 1 」进栈,因为它有左子树,读取左子树到最后一个左子树结点「 4 」,在这过程中将它们按序进栈,这时栈中的元素为「1, 2, 4 」。「 4 」出栈,读取它的右子树,重复上述操作,得到栈中元素为「 1, 2, 7 」。「 7 」出栈,因为结点「 7 」没有右子树,可视为已访问过其右子树,退回到结点「 7 」的父结点即结点「 4 」。因为「 4 」的左右子树都已被访问过,退回到其父结点「 2 」,「 2 」出栈,读取其右子树。
代码实现有两种方式。一种是比较复杂的,调用了栈的几个函数来实现该功能。
//中序遍历二叉排序树(非递归)
Status InOrderTraverse2(BiTree T)
{
SqStack S;
BiTree p;
p=(BiTree)malloc(sizeof(BiTNode));
InitStack(S); // 构建一个空栈
p=T;
while(p||!StackEmpty(S)) // StackEmpty( S ) 判断栈是否为空
{
if(p)
{
Push(S,p); // 入栈
p=p->lchild;
}
else
{
Pop(S,p); // 出栈
if(!PrintElement(p->data)) // 输出结点的值
return ERROR;
p=p->rchild;
}
}
printf("\n");
return OK;
}
第二种就很简洁了,不需要那么多个函数,几乎与我们的思路一模一样:
//中序遍历序列(非递归算法)
status M_nonrecursive(BTpoint T,Stack S)
{
while(T!=NULL||S.base!=S.top)
{
while(T!=NULL)
{
*S.top++=T;
T=T->lchild;
}
T=*--S.top;
Print_tree_data(T->data); // 输出结点的值
T=T->rchild;
}
return OK;
}
至于二叉树前序和后序遍历,基本上很容易就能推导出来了,因为二者遍历方式和二叉树中序遍历有许多的共通之处,在本站的数据结构和算法教程中,对二叉树遍历所有方式有一个完整的描述和整理,感兴趣的小伙伴可以前去观看,收集这些优秀的资料,化为己用,我们也能够实现知识积累的跨越。
选你想看
你适合学Java吗?4大专业测评方法
代码逻辑 吸收能力 技术学习能力 综合素质
先测评确定适合在学习
价值1998元实验班免费学












 在线咨询
在线咨询
 免费试学
免费试学