递归实现斐波那契数列
- 2022-08-05 09:56:55
- 675次 极悦
斐波那契数列是一系列数字,其中每个数字(前两个数字除外)都是前两个数字的总和。斐波那契数列通常从 0、1 开始。我们可以在 Java 中使用迭代或递归创建斐波那契数列。在本文中,我们将介绍在 Java递归方法中的斐波那契数列。
介绍
在斐波那契数列中,每个数字(前两个数字除外)都是前两个数字的总和。斐波那契数列的数学公式是:
F(n) = F(n - 1) + F(n - 2)F ( n )=F ( n-1 )+F ( n-2 )其中,F(n)表示n^{第}n时间_斐波那契数。
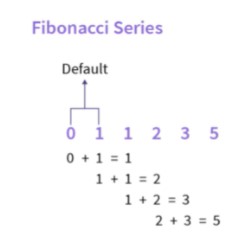
在 Java 中,我们可以使用递归和记忆等不同的技术来创建斐波那契数列。让我们看几个例子来了解我们如何创建斐波那契数列。
示例 1
在 Java 中使用递归的斐波那契数列 要在 Java 中使用递归计算斐波那契数列,我们需要创建一个函数以便执行递归。这个函数接受一个整数输入。该函数检查输入数字是0、1还是2,如果输入是三个数字中的任何一个,它分别返回0、1或1 。如果输入大于2,该函数会递归调用自身以获取先前的值,直到输入变量的值变得小于或等于2。因此,如果函数接收一个整数n作为输入,它将返回n^th^斐波那契数。要打印斐波那契数列,我们将调用此函数来计算每个斐波那契数。
public class FibonacciCalc {
public static int fibRecursion(int count) {
if (count == 0) {
return 0;
}
if (count == 1 || count == 2) {
return 1;
}
return fibRecursion(count - 1) + fibRecursion(count - 2);
}
public static void main(String args[]) {
int fib_len = 9;
System.out.print("Fibonacci Series of " + fib_len + " numbers is: \n");
for (int i = 0; i < fib_len; i++) {
System.out.print(fibRecursion(i) + " ");
}
}
}
程序的输出:
Fibonacci Series of 9 numbers is:
0 1 1 2 3 5 8 13 21
在上面的示例中,我们定义了一个递归函数fibRecursion来获取第 n 个斐波那契数并重复调用它(对于i=0 到 i=8),以创建一个长度为 9 的斐波那契数列。
时空复杂度
求解斐波那契数列的递归方法的时间复杂度为O(2^n)O ( 2n)即指数时间。如果我们考虑递归堆栈,递归方法的空间复杂度为O(n) 。
指数时间复杂度是极其低效的。使用递归方法计算长度很大的斐波那契数列需要很长时间。为了解决这个问题,我们可以使用记忆技术来创建斐波那契数列。这种技术比递归方法快得多。
示例 2
Java 中的斐波那契数与记忆记忆 记忆是一种用于提高递归程序性能的编程技术。在这种技术中,先前计算的结果被存储(缓存)并重复使用。在之前的方法中,我们分别计算每个斐波那契数。但是,在这种方法中,我们将使用之前的结果来计算当前的斐波那契数。因此,如果我们计算了一个数字的斐波那契,我们可以重复使用它而无需再次进行计算。
在之前的方法中,我们分别计算每个斐波那契数,但在这种方法中,我们将使用之前的结果来计算当前数字。
记忆化可以使用HashMaps来完成。
import java.util.HashMap;
import java.util.Map;
public class FibonacciCalc {
static private Map < Integer, Integer > memoizeTable = new HashMap < > ();
// Fibonacci with Memoization
static public int fibMemoize(int n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
if (memoizeTable.containsKey(n)) {
// getting value from the stored result(s)
return memoizeTable.get(n);
}
int result = fibMemoize(n - 1) + fibMemoize(n - 2);
// storing the result in cache
memoizeTable.put(n, result);
return result;
}
public static void main(String[] args) {
//FibonacciCalc fibo = new FibonacciCalc();
System.out.println("Fibonacci value for n = 6 --> " +
fibMemoize(6));
}
}
程序的输出:
Fibonacci value for n = 6 --> 8
在上面的例子中,我们创建了一个函数fibMemoize,它使用 memoization 来计算斐波那契数。在这个函数中,我们首先检查变量n 是 0 还是 1。如果n是0,我们返回 0 ,如果n是 1 ,我们返回1。如果n^{第}n时间_斐波那契数存储在 hashmap 中,我们直接使用它的值来获得所需的斐波那契数。如果没有存储n,我们通过调用前两个斐波那契值的函数来计算斐波那契值,然后将这个值存储到hashmap中,最后返回它来得到我们的答案。
时空复杂度
计算斐波那契数列的记忆方法的时间复杂度为O(n)。这种方法的空间复杂度也是O(n)。
以上就是关于“递归实现斐波那契数列”的介绍,大家如果想了解更多相关知识,可以关注一下极悦的Java教程,里面有更丰富的知识等着大家去学习,相信对大家一定会有所帮助的。
选你想看
你适合学Java吗?4大专业测评方法
代码逻辑 吸收能力 技术学习能力 综合素质
先测评确定适合在学习
价值1998元实验班免费学












 在线咨询
在线咨询
 免费试学
免费试学