平衡二叉查找树
- 2022-08-08 11:04:27
- 573次 极悦
平衡二叉树也称为高度平衡树。当左子树和右子树的高度之差不大于 m 时,它被定义为二叉树,其中 m 通常等于 1。树的高度是两棵树之间最长路径上的边数根节点和叶节点。
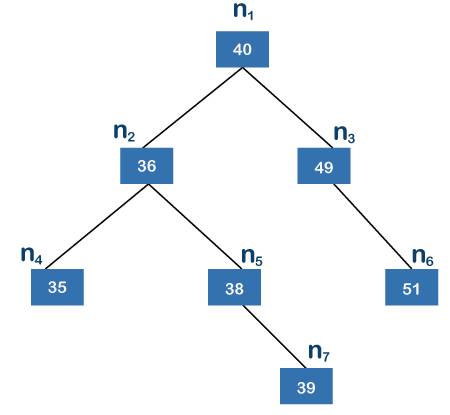
上面的树是二叉搜索树。二叉搜索树是一棵树,其中左侧每个节点的值都低于其父节点,而右侧节点的值高于其父节点。在上面的树中,n1 是根节点,n4、n6、n7 是叶子节点。n7 节点是离根节点最远的节点。n4 和 n6 包含 2 条边,根节点和 n7 节点之间存在 3 条边。由于 n7 离根节点最远;因此,上述树的高度为 3。
现在我们将看看上面的树是否平衡。左子树包含节点 n2、n4、n5 和 n7,而右子树包含节点 n3 和 n6。左子树有两个叶子节点,即n4 和n7。节点 n2 和 n4 之间只有一条边,节点 n7 和 n2 之间只有两条边;因此,节点 n7 离根节点最远。左子树的高度为2。右子树只包含一个叶子节点,即n6,并且只有一条边;因此,右子树的高度为 1。左子树和右子树的高度之差为 1。由于我们得到的值为 1,所以我们可以说上面的树是高度平衡的树。这个计算高度差的过程应该针对每个节点(如 n2、n3、n4、n5、n6 和 n7)执行。
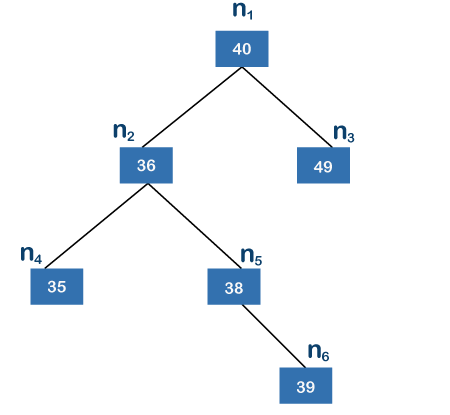
当我们处理每个节点时,二叉树在上面的树中,n6、n4 和 n3 是叶子节点,其中 n6 是离根节点最远的节点。根节点和叶子节点之间存在三条边;因此,上述树的高度为 3。当我们将 n1 视为根节点时,左子树包含节点 n2、n4、n5 和 n6,而子树包含节点 n3。在左子树中,n2 是根节点,n4 和 n6 是叶节点。在n4和n6个节点中,n6是离其根节点最远的节点,n6有两条边;因此,左子树的高度为 2。右子树的左右两侧确实有任何子树;因此,右子树的高度为0。由于左子树的高度为2,右子树的高度为0,所以左子树和右子树的高度差为2。根据定义,左子树和右子树的高度之差一定不能大于1。此时差为2,大于1;因此,上述二叉树是不平衡二叉搜索树。
为什么我们需要平衡二叉树?
让我们通过一个例子来了解平衡二叉树的必要性。

上面的树是二叉搜索树,因为所有左子树节点都小于其父节点,所有右子树节点都大于其父节点。假设我们想在上面的树中找到值 79。首先,我们将节点 n1 的值与 79 进行比较;由于 79 的值不等于 35 而大于 35 所以我们移动到节点 n3,即 48。由于值 79 不等于 48 并且 79 大于 48,所以我们向右移动48 的子节点。节点 48 的右子节点的值为 79,等于要搜索的值。搜索元素 79 所需的跳数为 2,搜索任何元素所需的最大跳数为 2。搜索元素的平均情况为 O(logn)。
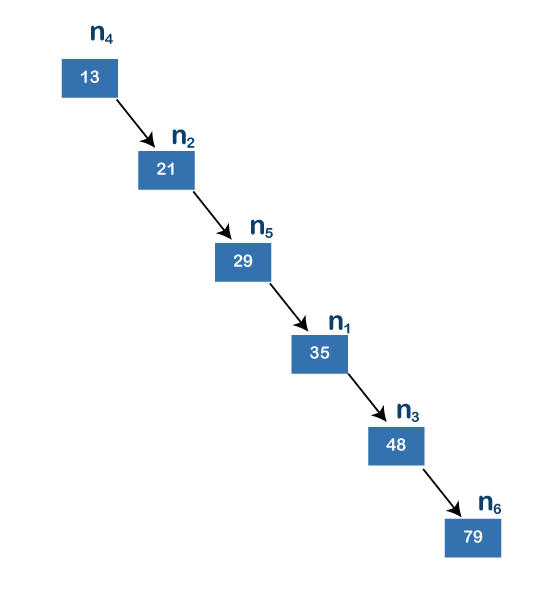
上面的树也是二叉搜索树,因为所有左子树节点都小于其父节点,所有右子树节点都大于其父节点。假设我们要在上面的树中找到值 79。首先,我们将值 79 与节点 n4 即 13 进行比较。由于值 79 大于 13,所以我们移动到节点 13 的右子节点,即 n2 (21)。节点 n2 的值为 21 小于 79,所以我们再次移动到节点 21 的右侧。节点 21 的右孩子的值为 29。由于值 79 大于 29,所以我们向右移动节点29的子节点。节点29的右孩子的值为35,小于79所以我们移动到节点35的右孩子,即48。值79大于48,所以我们移动到右孩子节点 48。48 的右子节点的值为 79,等于要搜索的值。在这种情况下,搜索一个元素所需的跳数是 5。在这种情况下,最坏的情况是 O(n)。
如果节点数增加,则树形图 1 中使用的公式比树形图 2 中使用的公式更有效。假设上述两棵树中可用的节点数均为 100,000。在树形图中搜索任何元素所需的时间为 100,000 µs,而在树形图中搜索元素所需的时间为 log(100,000),即 16.6 µs。我们可以观察到上述两棵树之间的巨大时间差异。因此,我们得出结论,平衡二叉树比线性树数据结构提供更快的搜索。
以上就是关于“平衡二叉查找树”的介绍,想学习更多的神奇的算法和数据结构,可以关注一下极悦的数据结构和算法教程,里面的课程内容细致全面,通俗易懂,是你的不二选择。
选你想看
你适合学Java吗?4大专业测评方法
代码逻辑 吸收能力 技术学习能力 综合素质
先测评确定适合在学习
价值1998元实验班免费学












 在线咨询
在线咨询
 免费试学
免费试学