浅谈森林的遍历

在计算机科学中，树（英语：tree）是一种抽象资料型别（ADT）或是实作这种抽象资料型别的数据结构，用来模拟具树状结构性质的资料集合。而森林是树的集合，由此可以对森林中的每一棵树依次从左到右进行先根遍历或者后根遍历。森林中的（第一棵树的根）、（第一棵树的子树森林）及（其余树构成的森林），分别对应为（二叉树的根）、（二叉树的左子树）和（二叉树的右子树），由此定义了森林的遍历方式。

森林的遍历操作有先序遍历和中序遍历两种方式：

1.先序遍历

如果森林非空，则：

访问第一棵树的根节点；

先序遍历第一棵树的根节点的子树森林；

先序遍历除第一个棵树之外，剩余的树构成的森林。

其访问顺序与该森林对应的二叉树的先序遍历顺序相同。

2.中序遍历

如果森林非空，则：

中序遍历第一棵树的根节点的子树森林；

访问第一棵树的根节点；

中序遍历除第一个棵树之外，剩余的树构成的森林。

其访问顺序与该森林对应的二叉树的中序遍历顺序相同。

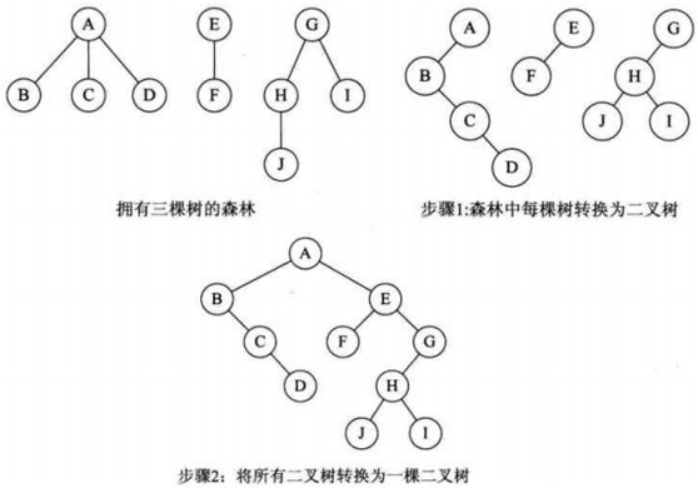
事实上，只有二叉树森林才有中序遍历与完整二叉树中序遍历对应，我们看这个森林和二叉树的各种遍历。

森林的先根遍历：A-B-C-D-E-F-G-H-J-I

二叉树森林的先序遍历：A-B-C-D-E-F-G-H-J-I(相同)

完整二叉树的先序遍历：A-B-C-D-E-F-G-H-J-I (相同)

森林的后根遍历：B-C-D-A-F-E-J-H-I-G

二叉树森林的后序遍历：D-C-B-A-F-E-J-I-H-G

完整二叉树的后序遍历：D-C-B-F-J-I-H-G-E-A(不同于二叉树森林的后序遍历)

二叉树森林的中序遍历：B-C-D-A-F-E-J-H-I-G(与森林的后根遍历相同)

完整二叉树的中序遍历：B-C-D-A-F-E-J-H-I-G(与森林的后根遍历相同，自然也与二叉树森林的中序遍历相同)

树的先根遍历即森林的先序遍历可对应到二叉树的先序遍历，树的后根遍历即森林的中序遍历可对应到二叉树的中序遍历。换句话说，若以孩子-兄弟链表作树（或森林）的存储结构，则树的先根遍历（或森林的先序遍历）的算法和二叉树的先序遍历算法类似，而树的后根遍历（或森林的中序遍历）的算法和二叉树的中序遍历算法类似。

以上就是本文对森林的遍历的讲解，其实道理很简单，森林是树的集合，那么森林的遍历也是以树的遍历为基础的。在本站的数据结构和算法教程中，还有对其他类型的数据结构的讲解，感兴趣的小伙伴可以丰富一下自己的数据结构知识。