![]() 二叉树面试题
二叉树面试题
树:树是由根节点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的节点,所定义的关系称为父子关系。
二叉树:树是由根节点和若干子树构成的。每个节点最多含有两个子树的树称为二叉树。
度:一个结点含有的子树的个数
叶子节点或终端节点:度为0的节点
节点的层数: 树根到节点的路径长度是该节点的层数,节点都有层数,根所在的层为0
树的高度或深度:树的高度或深度是树中节点的最大层数(最长路径的长度)加1 ,空树高度为0,只有根节点的树高度为1。
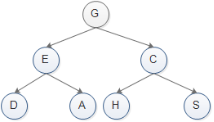
(1)先序遍历:先访问根节点,然后访问左子树,若当前节点无左子树,则访问当前节点的右子树;
如上图:
1.访问该二叉树的根节点,找到 G;
2.访问节点 G 的左子树,找到节点 E;
3.访问节点 E的左子树,找到节点 D;
4.由于访问节点 D左子树失败,且也没有右子树,因此以节点 D为根节点的子树遍历完成。 但节点 E 还没有遍历其右子树,因此现在开始遍历,即访问节点 A;
5.由于节点 A 无左右子树,因此节点 A 遍历完成,并且由此以节点 E 为根节点的子树也遍历完成。现在回到节点 G ,并开始遍历该节点的右子树,即访问节点 C;
6.访问节点 C 左子树,找到节点 H;
7.由于节点 H无左右子树,因此节点 H 遍历完成,回到节点 C 并遍历其右子树,找到节点 S;
8.节点 S 无左右子树,因此以节点 S为根节点的子树遍历完成,同时回归节点 G。由于节点 G 的左右子树全部遍历完成,因此整个二叉树遍历完成;
9.最终遍历的结果就是:GEDACHS
(2)中序遍历:先访问左子树,然后访问根节点,最后访问右子树,即左根右。所以遍历的结果是:DEAGHCS。
(3)后序遍历:先访问左孩子,然后访问右孩子,最后访问根节点,即左右根。所以遍历的结果是:DAEHSCG。
(4)宽度遍历:从根节点开始依次遍历左子节点和右子节点,直到所有子节点都变遍历完为止。所以遍历的结果是:GECDAHS。
1.前序遍历的第一个遍历节点必是根节点,而后序遍历的最后一个遍历节点必是根节点;
2.根据中序遍历顺序无法判断根节点,但若已知根节点,则可根据中序遍历顺序判断出左子树的组成元素和右子树的组成元素;
算法思路:
1.首先通过先序遍历【GEDACHS】或者后序遍历【DAEHSCG】可以得到二叉树的根节点G,通过中序遍历【DEAGHCS】可以得到左右子树的成员,即左子树的成员【DEA】,右子树的成员是【HCS】。
2.然后将左子树【DEA】看作新的二叉树,通过后序遍历【DAEHSCG】可以得到新二叉树的根节点为E。又通过中序遍历【DEAGHCS】可以得到A为E的右子树,D为E的左子树。
3.右子树HCS同理
依此类推,即可画出整棵二叉树。不难看出,画出这棵二叉树的顺序,就是我们想要得到的先序输出顺序,因此我们只需要在画二叉树时,对当前根节点进行输出,即可完成题目需要。这样只需要设置节点输出的位置就可以得到对应的遍历结果。
public class Node {
public int data;
public Node leftChild;
public Node rightChild;
public Node(int data) {
this.data = data;
}
}
public static void OrderTraveral(TreeNode node){
if(node == null){
return;
}
//递归前序遍历 根-> 左-> 右
/*
System.out.print(node.data+" ");
OrderTraveral(node.leftChild);
OrderTraveral(node.rightChild);*/
//递归中序遍历 左-> 根-> 右
/*
OrderTraveral(node.leftChild);
System.out.print(node.data+" ");
OrderTraveral(node.rightChild);*/
//递归后序遍历 左-> 右->根
/*
OrderTraveral(node.leftChild);
OrderTraveral(node.rightChild);
System.out.print(node.data+" ");*/
}
先序的思路:采用栈的先进后出思想进行实现的
1.首先有一个栈s1。
2.先将头结点入栈s1。
3.头结点出栈,判断当前结点的右孩子是不是为空,不为空则入栈;判断当前结点的左孩子是不是为空不为空则入栈。周而复始依次迭代。
public static void preOrder(Node head) {
System.out.print("pre-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
stack.add(head);
while (!stack.isEmpty()) {
head = stack.pop();
System.out.print(head.value + " ");
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
System.out.println();
}
中序的思路:采用栈的先进后出思想进行实现的
1.首先有一个栈s1。
2.判断头结点是不是为空,不为空则入栈s1,并获取头结点的左节点。如果为空则出栈头结点,并获取头结点的右节点。周而复始依次迭代。
public static void inOrder(Node head) {
System.out.print("in-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
while (!stack.isEmpty() || head != null) {
if (head != null) {
stack.push(head);
head = head.left;
} else {
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}
后序思路:
1.首先有两个栈s1和s2
2.先讲头结点入栈s1
3.栈s1的头结点出栈并入栈s2,判断当前结点的左孩子是不是为空,不为空则入栈s1;判断当前结点的右孩子是不是为空不为空则入栈s1。周而复始依次迭代,这样循环完后s2栈的入栈的顺序就是头右左;
4.将s2弹栈,周而复始依次迭代,弹出的顺序为左右头;
public static void posOrder(Node head) {
System.out.print("pos-order: ");
if (head != null) {
Stack<Node> s1 = new Stack<Node>();
Stack<Node> s2 = new Stack<Node>();
s1.push(head);
while (!s1.isEmpty()) {
head = s1.pop();
s2.push(head);
if (head.left != null) {
s1.push(head.left);
}
if (head.right != null) {
s1.push(head.right);
}
}
while (!s2.isEmpty()) {
System.out.print(s2.pop().value + " ");
}
}
System.out.println();
}
宽度遍历思路:
1.首先有一个队列queue1和一个levelMap
2.先讲头结点入队queue1
3.队列queue1的头结点出队并输出当前节点,判断当前结点的左孩子是不是为空,不为空则入队queue1;判断当前结点的右孩子是不是为空不为空则入队queue1。周而复始依次迭代;
public static void width(Node head) {
if(head == null) {
return 0;
}
Queue<Node> queue = new LinkedList<>();
queue.add(head);
while(!queue.isEmpty()) {
Node cur = queue.poll();
System.out.println(cur.value);
if(cur.left!=null) {
queue.add(cur.left);
}
if(cur.right!=null) {
queue.add(cur.right);
}
}
}
思路:
1. 首先有一个队列queue1,一个levelMap,一个遍历层数curLevel
2. 先将头结点入队queue1,并将头结点所在的层数存储到levelMap,一开始头节点在第一层所以levelMap.put(head, 1);
3. 队列queue1的头结点出队,获取头结点所在的层数curNodeLevel ,如果当前节点的层数curNodeLevel 和遍历的层数levelMap相等,则让当前层数的节点curLevelNodes自加1,否则就让遍历的层数curLevel自加1,并且当前层数的节点curLevelNodes初始化成1,确定最大宽度;判断当前结点的左孩子是不是为空,不为空则将该左孩子节点所在的层数存储到levelMap并入队queue1;判断当前结点的右孩子是不是为空不为空则将该右孩子节点所在的层数存储到levelMap入队queue1。周而复始依次迭代;
public static int w(Node head) {
if (head == null) {
return 0;
}
Queue < Node > queue = new LinkedList < > ();
queue.add(head);
HashMap < Node, Integer > levelMap = new HashMap < > ();
levelMap.put(head, 1);
int curLevel = 1;
int curLevelNodes = 0;
int max = Integer.MIN_VALUE;
while (!queue.isEmpty()) {
Node cur = queue.poll();
int curNodeLevel = levelMap.get(cur);
if (curNodeLevel == curLevel) {
curLevelNodes++;
} else {
max = Math.max(max, curLevelNodes);
curLevel++;
curLevelNodes = 1;
}
if (cur.left != null) {
levelMap.put(cur.left, curNodeLevel + 1);
queue.add(cur.left);
}
if (cur.right != null) {
levelMap.put(cur.right, curNodeLevel + 1);
queue.add(cur.right);
}
}
return max;
}
搜索二叉树是一种特殊有序的二叉树,如果一棵树不为空,并且如果它的根节点左子树不为空,那么它左子树上面的所有节点的值都小于它的根节点的值,如果它的右子树不为空,那么它右子树任意节点的值都大于他的根节点的值,它的左右子树也是二叉搜索树。
由此可见,如果对二叉搜索树进行中序排列(左中右),那么会得到一个从小到大的序列。
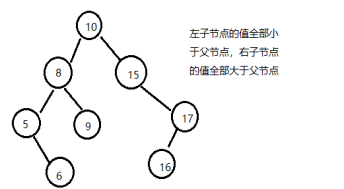
上图中序排列(左中右)后的顺序应该是:5,6,8,9,10,15,16,17。
具体思路:判断一棵树是不是搜索二叉树直接就是看中序遍历是不是升序,如果是升序就是搜索二叉树。
public static boolean checkBST2(Node head) {
List<Node> lst=new ArrayList<>();
process(head,lst);
//查看lst的顺序是否为升序的即可
}
public static void process(TreeNode head,ListNode lst){
if(node == null){
return;
}
//递归中序遍历 左-> 根-> 右
process(head.leftChild);
lst.add(head);
process(head.rightChild);
}
完全二叉树是由满二叉树而引出来的。对于深度为h 的,有N个结点的二叉树,当且仅当其每一个结点都与深度为h的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
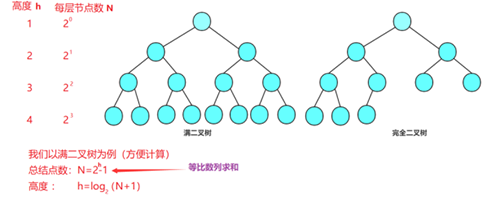
算法思路:
1.首先有一个队列queue,将头结点入队queue,
2.层序遍历的基础上,将头结点出队,获取该节点的左孩子和右孩子;
如果该节点的左孩子为空,右孩子不为空则返回false;
如果该节点的左右孩子不全为空,并且该节点不是叶子节点则返回false;
3.如果左孩子不为空,将左孩子入队;
4.如果右孩子不为空,将右孩子入队;
5.如果左右孩子都为空,将该节点设置为叶子节点;
6. 【2,3,4,5】步骤周而复始依次迭代;
7.最终返回true或者false;
public static boolean isCBT(Node head) {
if (head == null) {
return true;
}
LinkedList < Node > queue = new LinkedList < > ();
// 是否遇到过左右两个孩子不双全的节点
boolean leaf = false;
Node l = null;
Node r = null;
queue.add(head);
while (!queue.isEmpty()) {
head = queue.poll();
l = head.left;
r = head.right;
// 如果遇到了不双全的节点之后,又发现当前节点不是叶节点
if ((leaf && !(l == null && r == null)) ||(l == null && r != null)) {
return false;
}
if (l != null) {
queue.add(l);
}
if (r != null) {
queue.add(r);
}
if (l == null || r == null) {
leaf = true;
}
}
return true;
}
思路:
1.封装一个实体类,属性分别二叉树和树的高度。
2.因为拆分后的左子树和右子树的情况是一样的,都是判断自己的节点个数和树的高度。采用递归的方法获取树的节点个数和树的高度
3.将统计出的最大深度H和节点个数N,看是否满足N=2H-1。
public static class Info {
public int height;
public int nodes;
public Info(int h, int n) {
height = h;
nodes = n;
}
}
//=========
public static Info full(Node x) {
if (x == null) {
return new Info(0, 0);
}
Info leftData = full(x.left);
Info rightData = full(x.right);
int height = Math.max(leftData.height, rightData.height) + 1;
int nodes = leftData.nodes + rightData.nodes + 1;
return new Info(height, nodes);
}
//===========
public static boolean isF(Node head) {
if (head == null) {
return true;
}
Info data = f(head);
return data.nodes == (1 << data.height - 1);
}
1.任何一个节点的左子树或者右子树都是平衡二叉树。
2.任何一个节点的左子树高度和右子树高度差小于等于 1。
1.封装一个实体类,属性分别为是不是平衡二叉树和树的高度。
public static class ReturnType {
public boolean isBalanced;
public int height;
public ReturnType(boolean isB, int hei) {
isBalanced = isB;
height = hei;
}
}
2.采用递归的方法,因为拆分后的左子树和右子树的情况是一样的,都是判断自己是不是平衡二叉树和树的高度,通过判断各自是不是平衡二叉树以及计算树高度差是否小于等于 1。
public static ReturnType process(Node x) {
if (x == null) {
return new ReturnType(true, 0);
}
ReturnType leftData = process(x.left);
ReturnType rightData = process(x.right);
int height = Math.max(leftData.height, rightData.height) + 1;
boolean isBalanced = leftData.isBalanced && rightData.isBalanced && Math.abs(leftData.height - rightData.height) < 2;
return new ReturnType(isBalanced, height);
}
前驱节点:对一棵二叉树进行中序遍历,遍历后的顺序,当前节点的前一个节点为该节点的前驱节点;
后继节点:对一棵二叉树进行中序遍历,遍历后的顺序,当前节点的后一个节点为该节点的后继节点;
下面结构比普通二叉树节点结构多了一个指向父节点的parent指针。 如何在二叉算树中找到一节点的后继节点?
public class Node {
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int val) {
value = val;
}
}
思路:
1.获取该节点的右子树。
2.如果右子树不为空,获取该右子树的左子树,周而复始依次迭代,得到该右子树的最左边的节点,该节点就是所求的后继节点。
public static Node getLeftMost(Node node) {
if (node == null) {
return node;
}
while (node.left != null) {
node = node.left;
}
return node;
}
3.如果右子树不为空,获取该节点的父节点,判断父节点不为空且该节点是不是父节点的左孩子,周而复始依次迭代,如果是左孩子则该父节点就是所求的后继节点;
public static Node getSuccessorNode(Node node) {
if (node == null) {
return node;
}
if (node.right != null) {
return getLeftMost(node.right);
} else { // 无右子树
Node parent = node.parent;
while (parent != null && parent.left != node) { // 当前节点是其父亲节点右孩子
node = parent;
parent = node.parent;
}
return parent;
}
}