树数据结构面试题

001树的相关术语。

树：树是由根节点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的节点，所定义的关系称为父子关系。
二叉树：树是由根节点和若干子树构成的。每个节点最多含有两个子树的树称为二叉树。
度：一个结点含有的子树的个数
叶子节点或终端节点：度为0的节点
节点的层数： 树根到节点的路径长度是该节点的层数，节点都有层数，根所在的层为0
树的高度或深度：树的高度或深度是树中节点的最大层数（最长路径的长度）加1 ，空树高度为0，只有根节点的树高度为1。  

002二叉树有哪几种遍历方式。

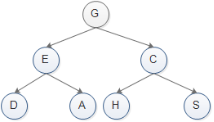
(1)先序遍历:先访问根节点，然后访问左子树，若当前节点无左子树，则访问当前节点的右子树；
如上图：
1.访问该二叉树的根节点，找到 G；
2.访问节点 G 的左子树，找到节点 E；
3.访问节点 E的左子树，找到节点 D；
4.由于访问节点 D左子树失败，且也没有右子树，因此以节点 D为根节点的子树遍历完成。 但节点 E 还没有遍历其右子树，因此现在开始遍历，即访问节点 A；
5.由于节点 A 无左右子树，因此节点 A 遍历完成，并且由此以节点 E 为根节点的子树也遍历完成。现在回到节点 G ，并开始遍历该节点的右子树，即访问节点 C；
6.访问节点 C 左子树，找到节点 H；
7.由于节点 H无左右子树，因此节点 H 遍历完成，回到节点 C 并遍历其右子树，找到节点 S；
8.节点 S 无左右子树，因此以节点 S为根节点的子树遍历完成，同时回归节点 G。由于节点 G 的左右子树全部遍历完成，因此整个二叉树遍历完成；
9.最终遍历的结果就是：GEDACHS
(2)中序遍历:先访问左子树，然后访问根节点，最后访问右子树，即左根右。所以遍历的结果是：DEAGHCS。
(3)后序遍历:先访问左孩子，然后访问右孩子，最后访问根节点，即左右根。所以遍历的结果是：DAEHSCG。
(4)宽度遍历:从根节点开始依次遍历左子节点和右子节点，直到所有子节点都变遍历完为止。所以遍历的结果是：GECDAHS。

003二叉树的遍历有什么规律？

1.前序遍历的第一个遍历节点必是根节点，而后序遍历的最后一个遍历节点必是根节点；
2.根据中序遍历顺序无法判断根节点，但若已知根节点，则可根据中序遍历顺序判断出左子树的组成元素和右子树的组成元素；

004二叉树遍历的递归实现。

算法思路：
1.首先通过先序遍历【GEDACHS】或者后序遍历【DAEHSCG】可以得到二叉树的根节点G，通过中序遍历【DEAGHCS】可以得到左右子树的成员，即左子树的成员【DEA】,右子树的成员是【HCS】。
2.然后将左子树【DEA】看作新的二叉树，通过后序遍历【DAEHSCG】可以得到新二叉树的根节点为E。又通过中序遍历【DEAGHCS】可以得到A为E的右子树，D为E的左子树。
3.右子树HCS同理
依此类推，即可画出整棵二叉树。不难看出，画出这棵二叉树的顺序，就是我们想要得到的先序输出顺序，因此我们只需要在画二叉树时，对当前根节点进行输出，即可完成题目需要。这样只需要设置节点输出的位置就可以得到对应的遍历结果。

public class Node {
    public int data;
	public Node leftChild;
	public Node rightChild;

	public Node(int data) {
		this.data = data;
	}
}
public static void OrderTraveral(TreeNode node){
    if(node == null){
        return;
    }
    //递归前序遍历   根-> 左-> 右
    /*
    System.out.print(node.data+" ");
    OrderTraveral(node.leftChild);
    OrderTraveral(node.rightChild);*/
    
    //递归中序遍历   左-> 根-> 右
    /*
    OrderTraveral(node.leftChild);
    System.out.print(node.data+" ");
    OrderTraveral(node.rightChild);*/
    
    //递归后序遍历   左-> 右->根
    /*
    OrderTraveral(node.leftChild);
    OrderTraveral(node.rightChild);
    System.out.print(node.data+" ");*/
}

005非递归实现二叉树的先序遍历。

先序的思路：采用栈的先进后出思想进行实现的
1.首先有一个栈s1。
2.先将头结点入栈s1。
3.头结点出栈，判断当前结点的右孩子是不是为空，不为空则入栈；判断当前结点的左孩子是不是为空不为空则入栈。周而复始依次迭代。

public static void preOrder(Node head) {
	System.out.print("pre-order: ");
	if (head != null) {
		Stack<Node> stack = new Stack<Node>();
		stack.add(head);
		while (!stack.isEmpty()) {
			head = stack.pop();
			System.out.print(head.value + " ");
			if (head.right != null) {
				stack.push(head.right);
			}
			if (head.left != null) {
				stack.push(head.left);
			}
		}
	}
	System.out.println();
}

006非递归实现二叉树的中序遍历。

中序的思路：采用栈的先进后出思想进行实现的
1.首先有一个栈s1。
2.判断头结点是不是为空，不为空则入栈s1，并获取头结点的左节点。如果为空则出栈头结点，并获取头结点的右节点。周而复始依次迭代。

public static void inOrder(Node head) {
	System.out.print("in-order: ");
	if (head != null) {
		Stack<Node> stack = new Stack<Node>();
		while (!stack.isEmpty() || head != null) {
			if (head != null) {
				stack.push(head);
				head = head.left;
			} else {
				head = stack.pop();
				System.out.print(head.value + " ");
				head = head.right;
			}
		}
	}
	System.out.println();
}

007非递归实现二叉树的后序遍历。

后序思路：
1.首先有两个栈s1和s2
2.先讲头结点入栈s1
3.栈s1的头结点出栈并入栈s2,判断当前结点的左孩子是不是为空，不为空则入栈s1；判断当前结点的右孩子是不是为空不为空则入栈s1。周而复始依次迭代，这样循环完后s2栈的入栈的顺序就是头右左；
4.将s2弹栈，周而复始依次迭代，弹出的顺序为左右头；

public static void posOrder(Node head) {
	System.out.print("pos-order: ");
	if (head != null) {
		Stack<Node> s1 = new Stack<Node>();
		Stack<Node> s2 = new Stack<Node>();
		s1.push(head);
		while (!s1.isEmpty()) {
			head = s1.pop();
			s2.push(head);
			if (head.left != null) {
				s1.push(head.left);
			}
			if (head.right != null) {
				s1.push(head.right);
			}
		}
		while (!s2.isEmpty()) {
			System.out.print(s2.pop().value + " ");
		}
	}
	System.out.println();
}

008非递归实现二叉树的宽度遍历。

宽度遍历思路：
1.首先有一个队列queue1和一个levelMap
2.先讲头结点入队queue1
3.队列queue1的头结点出队并输出当前节点，判断当前结点的左孩子是不是为空，不为空则入队queue1；判断当前结点的右孩子是不是为空不为空则入队queue1。周而复始依次迭代；

public static void width(Node head) {
	if(head == null) {
		return 0;
	}
	Queue<Node> queue = new LinkedList<>();
	queue.add(head);
	while(!queue.isEmpty()) {
		Node cur = queue.poll();
        System.out.println(cur.value);
		if(cur.left!=null) {
			queue.add(cur.left);
		} 
        if(cur.right!=null) {
			queue.add(cur.right);
		} 
	}
}