二叉搜索树之红黑树的实现

红黑树是一种二叉搜索树，每个节点都有一个额外的属性：颜色，它可以是红色或黑色。我们还需要跟踪每个节点的父节点，这样一棵红黑树的节点结构将是：

结构 t_red_black_node {
    枚举{红色，黑色}颜色；
    无效*项目；
    结构 t_red_black_node *left,
                     *正确的，
                     *父母;
    }

出于讨论的目的，终止树的 NULL 节点被认为是叶子，并被涂成黑色。

红黑树的定义

红黑树是一种二叉搜索树，具有以下红黑特性：

1.每个节点不是红色就是黑色。

2.每片叶子(NULL)都是黑色的。

3.如果一个节点是红色的，那么它的两个子节点都是黑色的。

4.从节点到后代叶子的每条简单路径都包含相同数量的黑色节点。

一个基本的红黑树

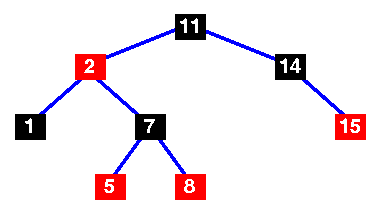
添加了哨兵节点的基本红黑树

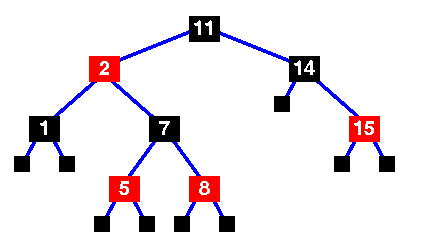
红黑树算法的实现通常包括哨兵节点，作为标记您已到达叶节点的便捷方式。它们是属性 2 的 NULL 黑色节点。

从但不包括节点x到叶子的任何路径上的黑色节点的数量称为节点的黑色高度，表示为bh(x)。我们可以证明以下引理：

引理

具有n 个内部节点 的红黑树的高度最多为 2 log( n +1)。

(有关证明，请参见 Cormen，第 264 页)

这说明了为什么红黑树是一棵好的搜索树：它总是可以在O(log n)时间内被搜索到。

与堆一样，红黑树的添加和删除会破坏红黑属性，因此我们需要恢复它。为此，我们需要查看一些对红黑树的操作。

旋转

旋转是搜索树中的局部操作，它保留了按顺序遍历键的顺序。

请注意，在两棵树中，有序遍历产生：

A x B y C

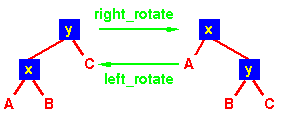
left_rotate 操作可以被编码：

left_rotate（树 T，节点 x）{
    节点 y;
    y = x->右；
    /* 将 y 的左子树变成 x 的右子树 */
    x->右=y->左；
    如果 ( y->left != NULL )
        y->左->父= x；
    /* y 的新父级是 x 的父级 */
    y->父= x->父；
    /* 设置父节点指向 y 而不是 x */
    /* 首先看看我们是否在根目录 */
    if ( x->parent == NULL ) T->root = y;
    别的
        if ( x == (x->parent)->left )
            /* x 在其父级的左侧 */
            x->父->左= y;
        别的
            /* x 必须在右边 */
            x->父->右=y；
    /* 最后，把 x 放在 y 的左边 */
    y->左= x；
    x->父母= y;
    }

插入

插入有些复杂，涉及多种情况。请注意，我们首先使用tree_insert函数在树中插入新节点x，就像我们对任何其他二叉树所做的那样。这个新节点被标记为红色，并且可能破坏了红黑属性。主循环向上移动树，恢复红黑属性。

rb_insert（树 T，节点 x）{
    /* 以通常的方式插入树中 */
    树插入（T，x）；
    /* 现在恢复红黑属性 */
    x->颜色=红色；
    while ( (x != T->root) && (x->parent->colour == red) ) {
       if ( x->parent == x->parent->parent->left ) {
           /* 如果 x 的父级是左，y 是 x 的右“叔叔”​​ */
           y = x->父->父->右；
           如果（y->颜色==红色）{
               /* case 1 - 改变颜色 */
               x->父级->颜色=黑色；
               y->颜色=黑色；
               x->父级->父级->颜色=红色；
               /* 在树上移动 x */
               x = x->父级->父级；
               }
           别的 {
               /* y 是一个黑色节点 */
               if ( x == x->parent->right ) {
                   /* 和 x 在右边 */
                   /* case 2 - 向上移动 x 并旋转 */
                   x = x->父级；
                   左旋转（T，x）；
                   }
               /* 案例 3 */
               x->父级->颜色=黑色；
               x->父级->父级->颜色=红色；
               right_rotate(T, x->parent->parent);
               }
           }
       别的 {
           /* 左右重复“if”部分
              交换*/
           }
       }
    /* 将根着色为黑色 */
    T->根->颜色=黑色；
    }

以上就是关于“二叉搜索树之红黑树的实现”介绍，大家如果对此比较感兴趣，不妨来看看简述数据结构中7种树，里面有更多的相关知识可以学习，相信对大家一定会有所帮助的。